Convexity

Convexity (in bonds) measures how the duration of a bond changes as interest rates move. Bond prices across durations don’t move in straight lines when rates change. The relationship is curved, and convexity captures that curvature.

Why Convexity Matters in Bond Analysis:

• More Accurate Risk Measure:
  Duration alone can misestimate price changes for large rate moves. Convexity adds precision by accounting for the curve in bond price behavior.
• Interest Rate Sensitivity:
  Bonds with higher convexity will gain more in price when rates fall and lose less when rates rise, making them more attractive in volatile rate environments.
• Portfolio Strategy:
  Fixed-income managers often prefer higher convexity bonds (like long-term zero-coupon bonds or mortgage-backed securities) when expecting rate volatility, as they provide better protection and upside.
• Cost Trade-Off:
  Higher convexity bonds usually come with lower yields, since investors are willing to pay a premium for the favorable risk-return profile.

Here’s a simple way to visualize all this:

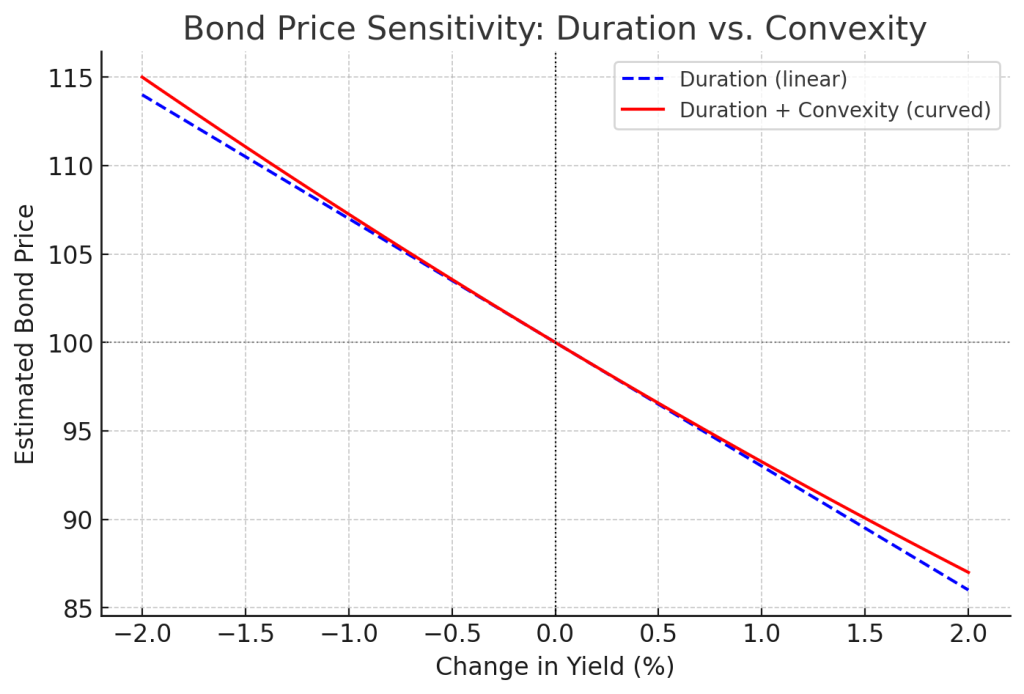
In the chart above:

• Duration (blue dashed line) gives you a straight-line estimate of how much a bond’s price will change if interest rates move. Duration = speed of price change.
• Convexity (red curved line) adjusts that estimate to reflect the curve in reality – bond prices don’t move in a straight line. Convexity = acceleration of price change (curve of the ride).

Bottom Line:
Convexity is an advanced but essential tool for understanding bond price behavior beyond duration. It helps investors better gauge interest rate risk, compare bonds, and build resilient fixed-income portfolios.